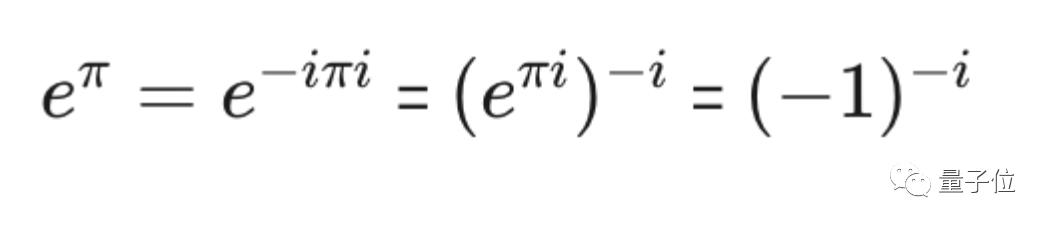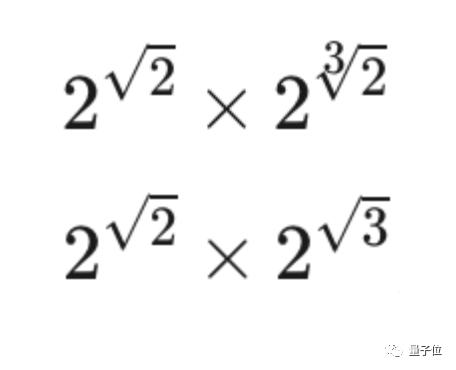Fengse compiled from the concave temple
Quantum bit | WeChat official account QbitAI
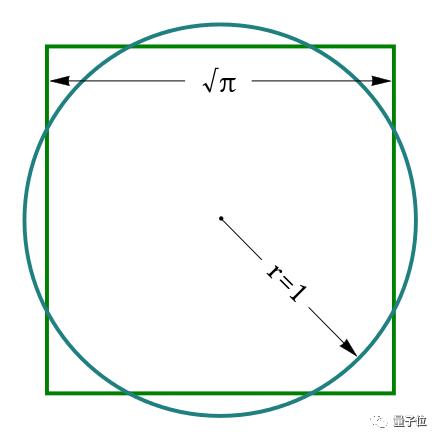
In the history of mathematics, there is a famous problem of "turning a circle into a square".
It was put forward by an ancient Greek philosopher in prison in the 5th century BC. It is about drawing a square with a compass and a scaleless ruler to make its area equal to that of the circle.
However, no one expected that this problem has been puzzling mathematicians for more than 2000 years.
In the end, it was discovered by everyone, and it was impossible to draw it.

The reason is related to π being a transcendental number-
Yes, π is a transcendental number besides the irrational number identity known to primary school students.
When it comes to transcendental number, it’s a really hard concept to understand, and no number of professional textbooks can make it easy to understand.

It can only be said that it is a class of irrational numbers, but it is more "unreasonable" than irrational numbers. .
From the 18th century to the present, back and forth for more than 200 years, a large number of mathematicians from various countries have pounced on it, looking for evidence to prove its existence and ways to judge it.
However, this "little thing" is so elusive that until now there are still many suspected figures that have not been proved and a lot of open problems related to it have not been solved.
"Terrible" is that many mathematicians said:
In fact, I know that it is useless to find out which number is beyond the number, but I just can’t stop!

Therefore, today’s article is a dry issue of mathematics, which comes from the column of Quanta Magazine (author David S. Richeson). It is the most clear and easy-to-understand article that tells the ins and outs of transcendental numbers, and is hereby compiled.

Then, blessed are those who like mathematics today-
Love beyond a few times again, and see how it was discovered by mathematicians and how it was related to that Millennium problem.
The Unsolvable Problem of "Turning a Circle into a Square"
Mathematician Leopold Kronecker famously said:
God himself created natural numbers, and the rest came from human power.
Nowadays, although all kinds of numbers have a fascinating and complicated history, basically everyone has a clear definition of them.
For example, integers are positive integers and zero plus negative integers. Rational number is a number that can be expressed as the ratio of two integers, including integers, finite decimals and infinite cyclic decimals.
If the decimal places of this ratio are never divided and never repeated, it is an irrational number.
Then rational numbers and irrational numbers together form real numbers, and real numbers and imaginary numbers form complex numbers.
Among them, today, we all agree that rational numbers were discovered by hippasus, who lived around the 5th century BC (and he died because of it).
But in fact, his discovery belongs to geometric meaning rather than arithmetic.
He proved that you can find two line segments that cannot be divided into several equal lengths, such as the sides and diagonals of a square.
Today we call this incommensurability, which means that their lengths are not rational multiples of each other.
Therefore, the diagonal length of a square is √2 times the side length, and this √2 is called an irrational number.
Undoubtedly, using compasses and straightedge, we can draw a line segment with any positive rational length.
However, some unreasonable lengths are also acceptable. For example, in the famous golden ratio (1+√5)/2, draw a regular Pentagon with a side length of 1 and take its diagonal.
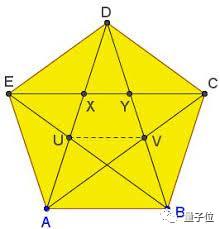
In 1637, the famous mathematician Descartes proved:
As long as a number can be represented by integer operations of addition, subtraction, multiplication, division and square root, then we can draw the corresponding line segments (such as all positive rational numbers, as well as the √2 and the golden ratio just mentioned).
Therefore, if we can express π with an exact formula, can we solve the problem of "turning a circle into a square"!
The problem is, I can’t find it.

In a blink of an eye, 200 years have passed (two centuries have passed).

A French mathematician named Pierre Wantzel finally proved:
If a number can be drawn by line segments, that is, it can be constructed, then it must also be the root of a polynomial that cannot be further factorized or simplified, and the degree of the highest term of this polynomial is a power of 2 (such as 2, 4, 8, 16, etc.).
For example:
√2 is the root of the polynomial x2–2, and the golden ratio is the root of x2–x–1, so they can all be drawn.
And like 3; √2 is the root of the polynomial x3–2, which does not meet the condition of the second power, so it is impossible to draw a line segment of this length.
However, even if we know this law, we still haven’t found the exact expression of π, and the problem of turning a circle into a square is still unresolved.
It was finally proved that it could not be drawn at all.
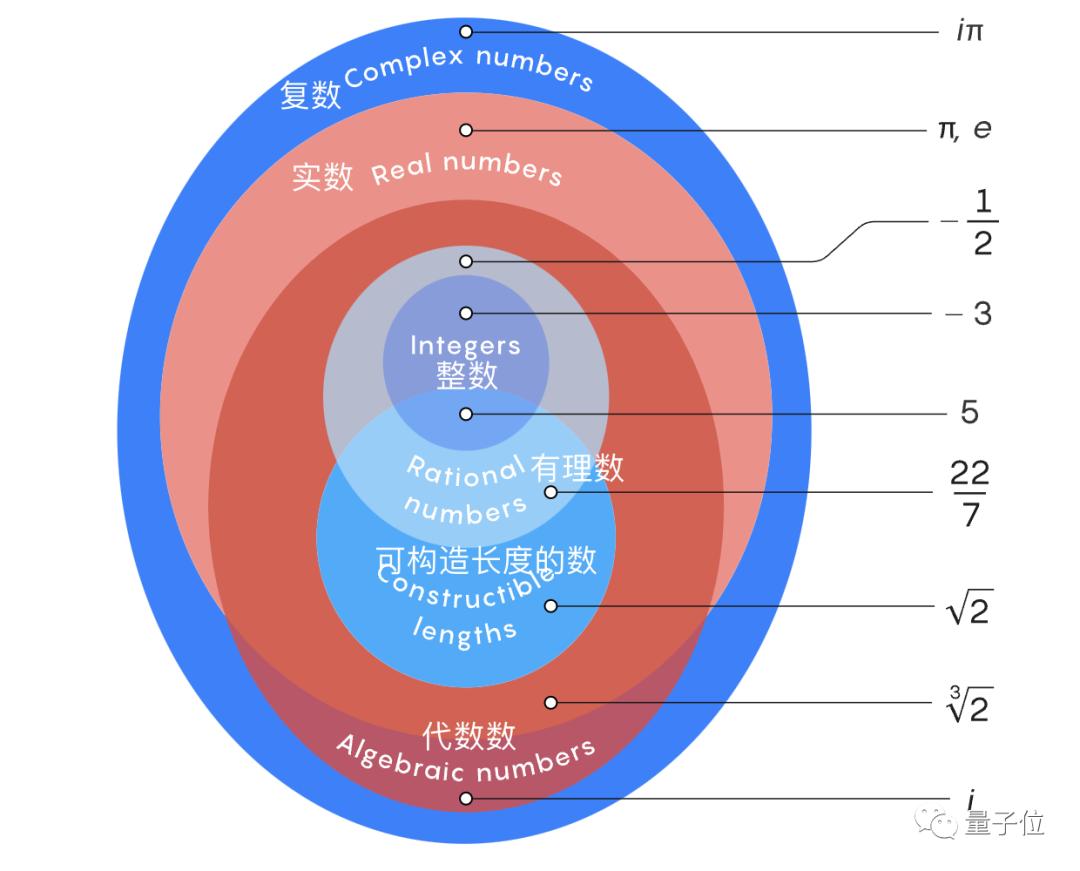
In fact, the key to solving the problem of turning a circle into a square is just like mathematicians divided real numbers into rational numbers and irrational numbers before-complex numbers need to be divided into two sets.
For complex numbers, many of them are equal to the roots of polynomials with integral coefficients, which mathematicians call algebraic numbers.
Every rational number is an algebraic number, and so are some irrational numbers, such as 3; √2, and even the imaginary number I, it counts, because it is the root of x2+1.
Not all complex numbers are like this, so the values that do not belong to this category are called transcendental numbers.
However, it is not obvious whether a transcendental number exists, and it is also very challenging to prove whether a given number is transcendental, because it is necessary to disprove that a number is not the root of any integer coefficient polynomial.
The first breakthrough point was born in 1844, and a French mathematician named joseph liouville thought of such an indirect method:
Since irrational numbers can’t be well approximated by rational numbers, if I find a number that can be infinitely approximated by fractions with smaller denominators, it must be something else: transcendental numbers.
So, Joseph Liouville constructed such a number:
L=0.1100010000000000000000010…
It has only 0 and 1, where the position of 1 appears in turn by "n!" Decide that the position of the first 1 is equal to "1!" , that is, 1, and the second is equal to "2!" , appears in the second place, and the third is equal to "3!" , in the sixth place, and so on.
This ingenious design makes the scores of 1/10, 11/100 and 110001/1000000 very close to the value of L itself.
This proves the existence of transcendental numbers (that is, he created this L).

However, the number π does not satisfy Joseph Liouville’s condition (it cannot be infinitely approximated by rational numbers), so it is not clear whether π is beyond the number.
The important breakthrough came in 1873, nearly 30 years later.
A French mathematician named Charles Hermite designed a clever method to prove that the base e of natural logarithm is transcendental.
This is the first transcendental number that is not artificially designed, which makes Lin Deman, a German mathematician, finally prove that π is a transcendental number on the basis of his theory nine years later.
First, he proved that as long as D is a nonzero algebraic number, ed is a transcendental number.
In other words, if ed is an algebraic number, but d is either 0 or transcendental.
In this case, based on Euler’s identity, which is recognized as the most perfect formula in mathematics, eπ i = 1, the category of π can be deduced.
Because -1 is an algebraic number, πi must be a transcendental number based on the theorem just now, and π must be transcendental because I is also an algebraic number.
In this way, "big things are not good"-
π is a transcendental number, which means π does not meet the definition of "line segment that can be drawn" mentioned in the previous paragraph, so the problem of turning a circle into a square put forward by ancient Greek philosophers thousands of years ago is impossible to realize.

The story is not over yet.
The story of turning a circle into a square is over, but the exploration of transcendental numbers has just begun.
Shortly after E was proved to be a transcendental number, another mathematician proved that infinite numbers actually have different sizes, but the infinity of rational numbers is the same as the infinity of integers. Such a set is called "countably infinite".
However, the set of real numbers and irrational numbers is larger, which is uncountable infinity; At the same time, although the algebraic number set contains all rational numbers and infinitely many irrational numbers, it is still an infinitely small and countable infinite set.
Therefore, its complement, that is, transcendental number, is uncountable and infinite.
In other words, most real numbers and complex numbers are transcendental numbers.

-Although there are so many excesses, by the turn of the 20th century, mathematicians could only identify a few of them.
In 1900, the famous German mathematician David Hilbert listed a famous list of 23 most important unsolved mathematical problems, the seventh of which was:
It is proved that when A is an algebraic number and is not equal to 0 or 1, and B is an algebraic irrational number, ab is a transcendental number.
In 1929, Aleksandr Gelfond, a young Russian mathematician, proved that B = I √ r and r are special cases of positive rational numbers, which means that eπ is a transcendental number.
This result is surprising, because according to the theorem, e and π are not algebraic numbers.
However, by manipulating Euler’s identity skillfully again, we know what’s going on:
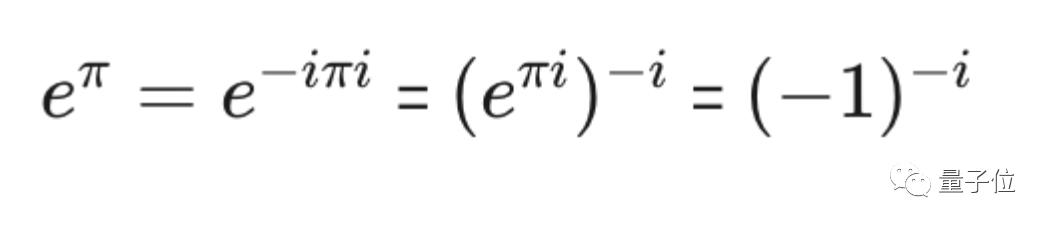
Soon after, another mathematician discovered that 2√2 was a transcendental number. Then, the seventh problem listed by David Hilbert was solved by two mathematicians independently.
Later, Alan Baker, a mathematician, published a series of articles, summarizing the achievements of these people, which made us have a deeper understanding of transcendental numbers, and therefore won the Fields Prize in 1970.
Of course, at the age of 31, his greatest achievement in winning this honor is to prove that two values such as the following are also transcendental numbers:
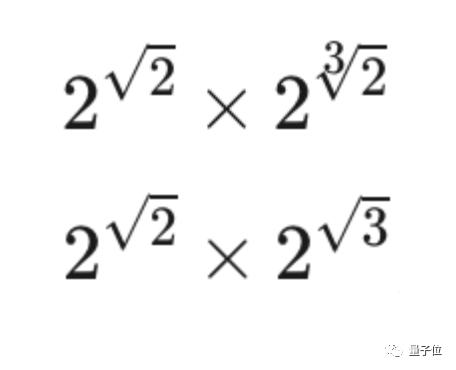
Until now, there are many open questions about transcendental numbers, and there are many concrete numbers that seem to be "very transcendental", which have never been proved, such as "eπ", "e+π", "ee", "π π" and "π e".
But as said at the beginning, the mathematician said:
It may not be useful to know who is above the number, but if we have the ability to know but choose not to know, it is definitely unacceptable.
Seriously respect.

Original link:
How Math Achieved Transcendence
End—
Advances in science and technology meet every day ~
Original title: "The irrational number in this irrational number makes mathematicians call" it can’t stop at all ""
Read the original text